Acid base titration - titration curve calculation
We have already described two exact methods of acid-base titration curve calculation on ChemBuddy site. Both methods are difficult to use if calculations are to be done manually. One gives high degree polynomials that have to be solved, the other is much more straightfoward, but it is still rather elaborate and allows calculation of volume of titrant as a function of pH, which is exactly opposite of what we usually need. However, in most cases these methods are overkill and you should use simplified approach, using different approaches to different types of titrations and different areas of the curve. To summarize:
- In the case of titration of strong acid (base) we assume that pH is controlled just by the concentration of the not neutralized titrated substance before end point, and by the excess of titrant after end point. Near the endpoint you may use equation 7.4 of ChemBuddy pH calculation lectures to take water dissociation into account, or - if there is no need for so precise results - you may assume endpoint pH to be 7.00.
- For the titration of the weak acid (or base) using strong neutralizing agent starting point pH is just pH of a weak acid (base) solution (see equation 8.10 or 8.13), acid base titration curve before endpoint is described by Henderson-Hasselbalch equation, for endpoint pH is calculated as for a salt solution (calculate pOH from the concentration of conjugate base or pH from concentration of conjugate acid), further values are calculated from the (strong) titrant excess.
- Finally for the titration of weak acid (base) using weak base (acid) equation 11.13 (or 11.16) must be used. Such titrations are never done in laboratory practice. Calculations are not easy and this is one of the cases when use of some kind of pH calculator is a must.
Just in case we will show here again how to derive the simplest formula allowing calculation of volume of base added to acid, if we know pH of the solution. This formula will come handy in the discussion of the end point detection.
We assume strong acid or base is used as a titrant.
First step is as usual calculation of concentrations of all substances entered into the solution. What we do next depends on the titrated substance.
If the titrated substance is strong (fully dissociated) we assume the neutralization reaction to proceed quantitatively - and pH depends only on the amount of excess of titrated substance (before the equivalence point) or excess of titrant (after the equivalence point). Equivalence point pH is 7.00 (unless ionic strength and activities are taken into account). Very close to the equivalence point water dissociation have to be accounted for (for details see pH of any monoprotic acid or base solution and pH of strong acid or base solution).
If - still in the case of strong acid HA and strong base BOH - we want to proceed in the reverse direction - calculate volume of titrant for a given pH, we will make the same assumption that neutralization went to completion. We will also assume both acid and base to be completely dissociated. That means that the solution is described by just two equations. One is charge balance:
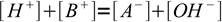 1
1the other one water ion product:
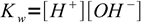 2
2Let VA be initial volume of the acid, CA its initial concentration, VB volume of the titrant added and CB its concentration. If so, concentrations of A- and B+ are
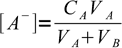 3
3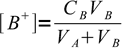 4
4All above equations can be combined:
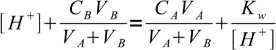 5
5We want to find out volume of titrant added and its the only unknown, one that the equation can be easily solved for:
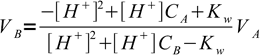 6
6It may happen that calculated VB is negative - that is a sure sign, that pH value used for calculation of [H+] is outside of the values observed during titration in which acid and base of concentrations CA and CB respectively are used.
If the titrated substance is weak calculation of pH before end point is done using Henderson-Hasselbalch equation describing pH of buffer solutions. To do so we assume that neutralization went to completion and we calculate concentration of the weak acid (base) and its conjugate base (acid) treating titrant as a limiting reagent. There is no need to use ICE table (this is a very common error). pH at equivalence point is calculated as effect of hydrolysis of the salt, and pH after the equivalence point depends solely on the titrant excess.
Titration curves of polyprotic acids are much harder to calculate. Equation derived above is universal, and describes any titration curve, but its direct application is cumbersome. At the same time manual calculation of the pH of multiprotic acid mixed with a base requires much more skill and experience, and is not always possible, as quite often it requires solving high degree polynomials. Thus - while in some cases it is possible to calculate at least parts of the curve using methods described in ChemBuddy pH calculation lectures - it is much better to use specialised software, like pH calculator. You will not only save time, but also gain on calculations accuracy.
What is pH of 0.1023 M HCl solution titrated 75% with 0.08976 M solution of NaOH?
After the solution has been titrated 75% there is 25% of original strong acid left. However, this acid is diluted by the titrant addition. Let's assume we have started with VHCl mL of acid and its concentration was CHCl. Let's name volume of base added VNaOH and base concentration CNaOH.
Initially there were
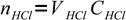 7
7moles of acid. It is titrated 75% so we have added
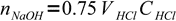 8
8moles of base. This amount is found in
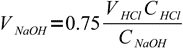 9
9Total volume of the solution is
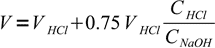 10
10and actual concentration of acid left is
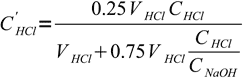 11
11Note, that VHCl cancels out and we are left with
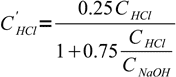 12
12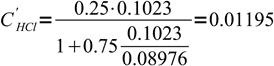 13
13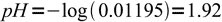 14
14Calculate pH of the 0.1012 M acetic acid solution after 5.14 mL of 0.1231 M NaOH have been added to 25 mL sample. pKa = 4.75.
First of all we will convert given information to titration fraction.
We started with 25 mL of 0.1012 M acetic acid solution, that is 0.025×0.1012=0.00253 moles of acid (2.53 mmoles). To that we have added 5.14 mL of 0.1231 M NaOH solution, that is 0.00514×0.1231=6.33×10-4 moles of base. As acetic acid reacts with sodium hydroxide 1:1:
CH3COOH + NaOH → CH3COONa + H2O
we can easily calculate that 6.33×10-4/0.00253=0.25 (25%) of acid was neutralized.
As we have explained earlier, for a weak acid titration it is best to use Henderson-Hasselbalch equation:
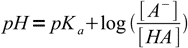 15
15We know 25% of the acid was neutralised, that means 75% is still intact. Note, that we don't have to calculate exact concentrations of acid and conjugate base, as we are interested only in their ratio. Even if we will express exact concentrations by initial concentration, titration percentage and solution volume, everything but titration percentage will cancel out (try to check it by yourself). Thus we can just plug known numbers into the equation:
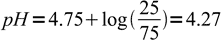 16
16And 4.27 is the final answer.





